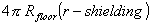
Appendix A - Design Calculations

i)                    Torus

Floor area required at 1g: 1,442,640m²

Floor area of torus: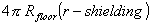

Where     = radius to torus floor

            r           = minor radius

Rotation rate required to get 1g acceleration at torus floor: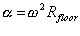

Where          = acceleration due to gravity (9.806ms­^-2)

                    = angular velocity (rad/sec)

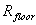               = radius to torus floor

Limit of rotation rate: 1 rpm = 0.1047 rad/sec

=> minimum radius to torus floor: 894.5m

=> maximum minor radius: 128m (+ radiation shielding)

Line of sight (i.e. - how far you can see before floor reaches eye level)

Equation of a circle: x² + y² = r²

Where x and y are co-ordinates of point, i.e. - ordered pair (x, y) and r = radius of circle

For line of sight, x = radius - height above floor (1.7m),  r = radius to torus floor

=> Line of sight (y) =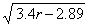

Comparison of radii

ii)                   Moveable spheres (see fig. 7.1b)

Floor area required: 9,000m²  (2,250m² per sphere)

Door to lift: every 18m

Area of sleeves: 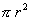 = 86.59m² in each floor

Floor 2 (door at centre) => floor 1.5m below equator.

x² + y² = r²

=>        x² = r ² - (1.5)²

=> Floor area =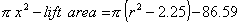

Floor 1, 16.5m above equator

Floor area =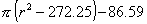

Floor 3, 19.5m below equator

Floor area =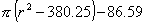

Floor area required = S floor areas 1, 2, 3

=>2250 =

=> r ²    =  484.545

    r       =  22m

Previous Section

Return to Index

Next Section